phi five alpha omega

Goldberg_polyhedra

Ho-Mg-ZnQuasicrystal

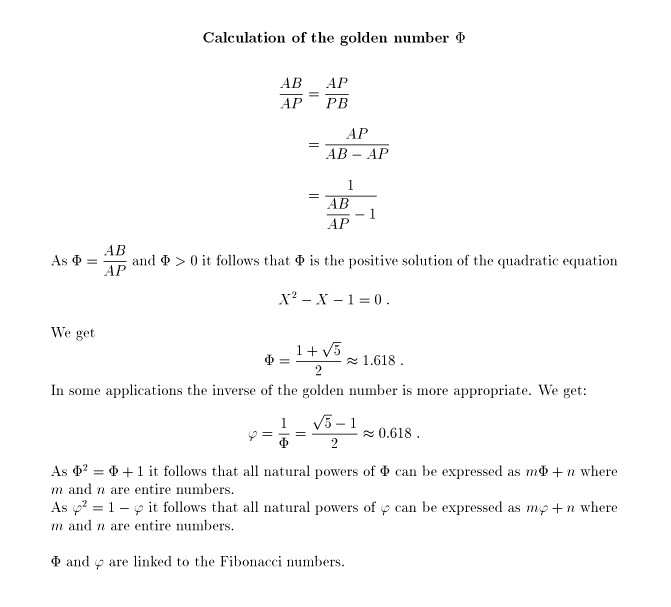
A structure analysis of Zn-Mg-Ho icosahedral quasicrystal

        public static MeshDraft Dodecahedron(float radius)
        {
            float magicAngle1 = Mathf.PI*52.62263590f/180;
            float magicAngle2 = Mathf.PI*10.81231754f/180;
            float segmentAngle = Mathf.PI*2/5;
            float currentAngle = 0f;
            var lowerCap = new List<Vector3>();
            var lowerRing = new List<Vector3>();
            for (var i = 0; i <= 5; i++)
            {
                lowerCap.Add(PTUtils.PointOnSphere(radius, currentAngle, -magicAngle1));
                lowerRing.Add(PTUtils.PointOnSphere(radius, currentAngle, -magicAngle2));
                currentAngle -= segmentAngle;
            }

            currentAngle = -segmentAngle/2;
            var upperCap = new List<Vector3>();
            var upperRing = new List<Vector3>();
            for (var i = 0; i <= 5; i++)
            {
                upperCap.Add(PTUtils.PointOnSphere(radius, currentAngle, magicAngle1));
                upperRing.Add(PTUtils.PointOnSphere(radius, currentAngle, magicAngle2));
                currentAngle -= segmentAngle;
            }

            var draft = TriangleFan(lowerCap);
            draft.Add(FlatBand(lowerCap, lowerRing));
            draft.Add(FlatBand(lowerRing, upperRing));
            draft.Add(FlatBand(upperRing, upperCap));
            upperCap.Reverse();
            draft.Add(TriangleFan(upperCap));
            draft.name = "Dodecahedron";
            return draft;
        }

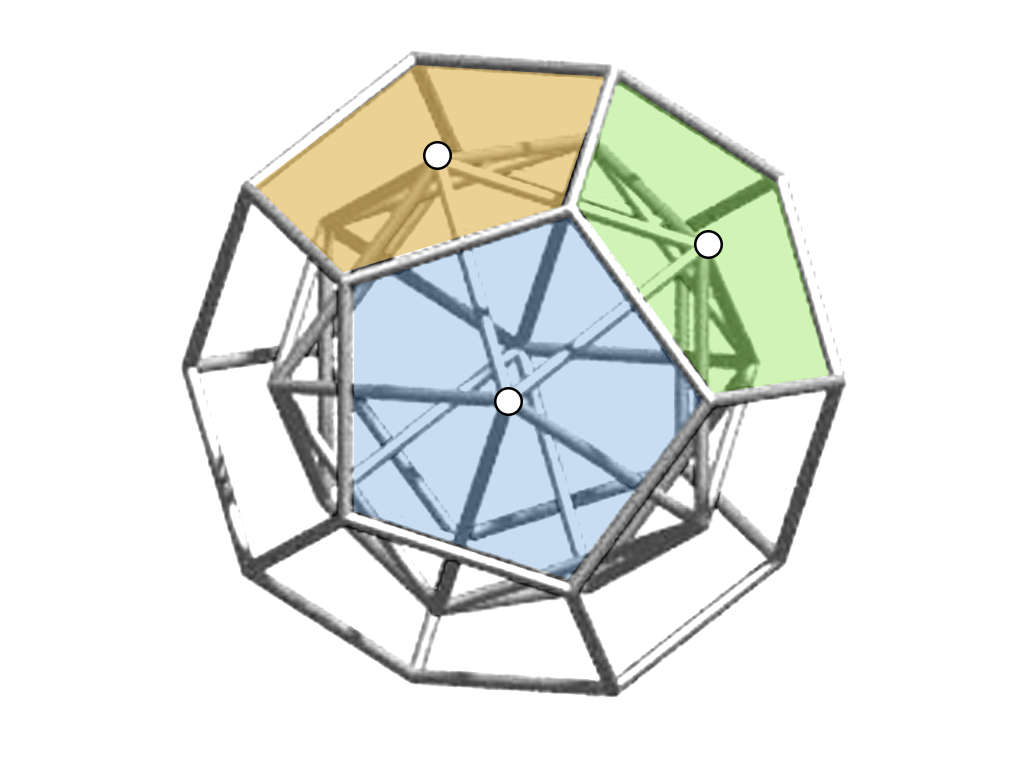
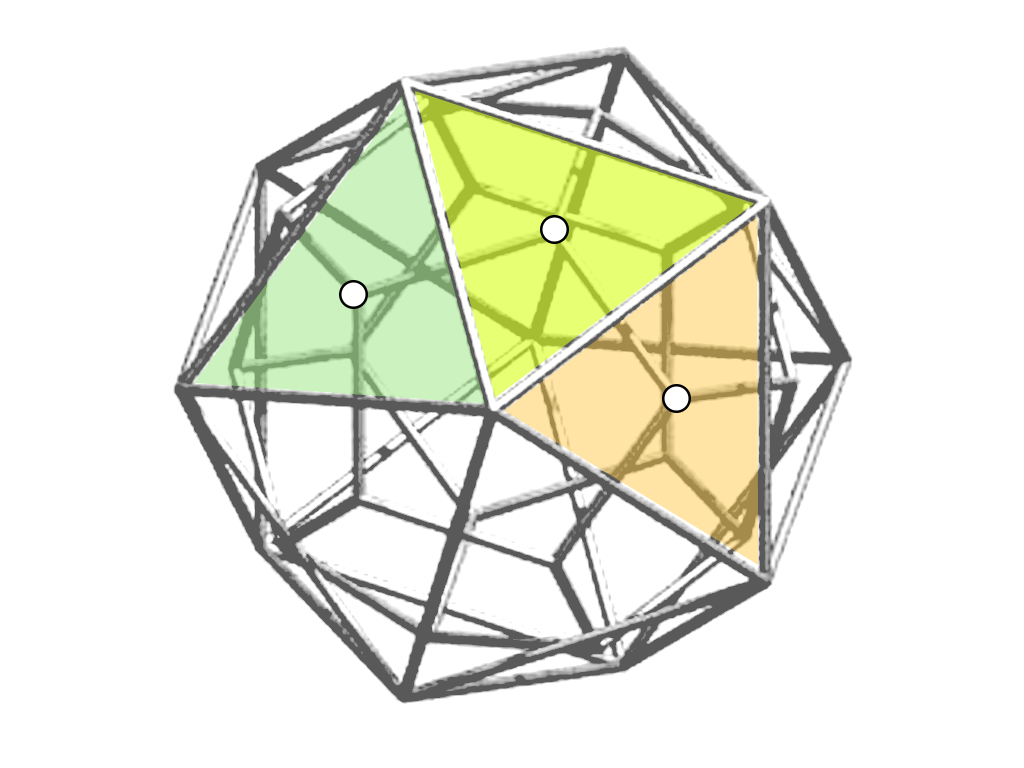
Dual Polyhedra

The centers of the faces of a regular dodecahedron are the vertices of a regular icosahedron and the centers of the faces of a regular icosahedron are the vertices of a regular dodecahedron.
Both regular polyhedra are “dual polyhedra”.

doe_cos)hfjhgfjf

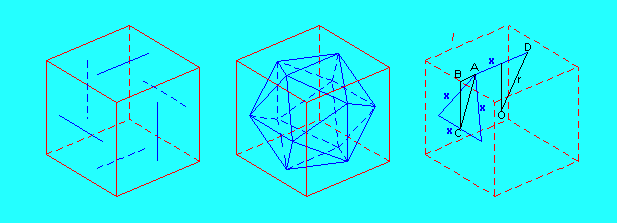
icosa01

icosa02

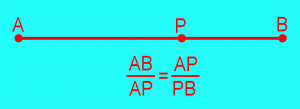
In Golden section – Pentagon – Dodecahedron the a regular dodecahedron can be constructed starting from a cube and what relation exists between the edge of this dodecahedron and the edge of the given cube.
The ratio edge of the dodecahedron / edge of the cube is the inverse of the golden number Phi. If we consider also a second cube, “circumscribing” the dodecahedron the ratio of the edge of the dodecahedron and the edge of this second cube is the inverse of the square of Phi.

The same circle circumscribes both the pentagon of the dodecahedron and the triangle of the icosahedron inscribed in the same sphere.

icos01