Goldberg Variations

 

 

 
Understanding Quaternions

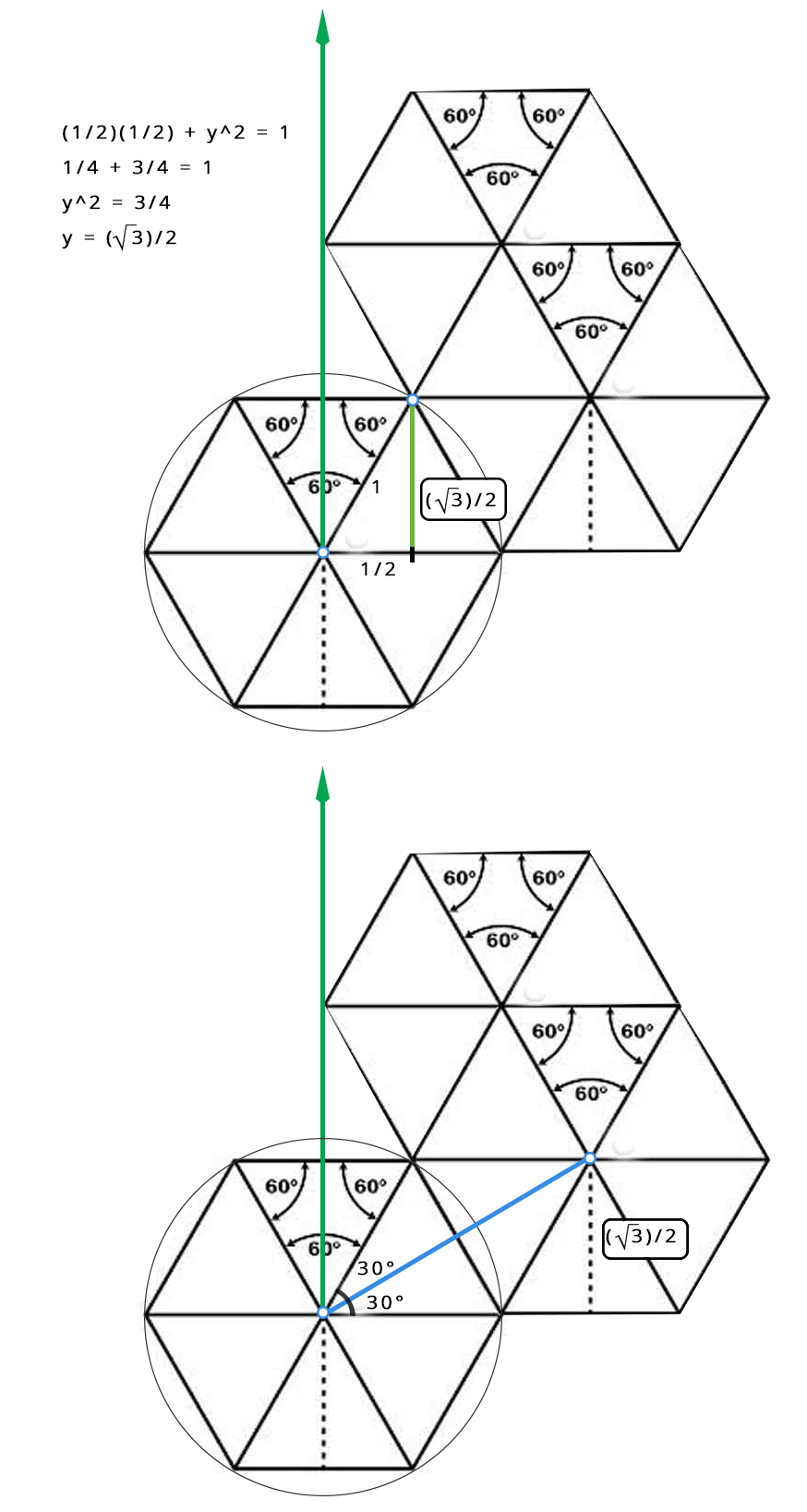
Unit Quaternion

Given an arbitrary vector v, we can express this vector in both its scalar magnitude and its direction as such:

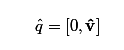
And combining this definition with the definition of a pure quaternion gives:

And we can also describe a unit quaternion that has a zero scalar and a unit vector as such:

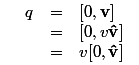
a quaternion

is a quantity which represents a rotation. If you need a physical meaning then this is probably the best way to think of it:

q = cos(a/2) + i ( x * sin(a/2)) + j (y * sin(a/2)) + k ( z * sin(a/2))

where:

• a=angle of rotation.
• x,y,z = vector representing axis of rotation.

So it is closely related to the axis angle representation of rotations.

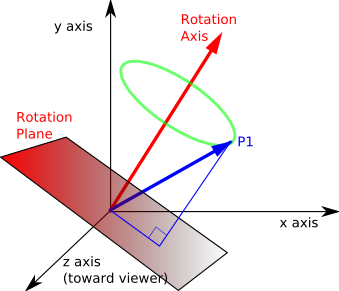
In the following diagram:

• Rotation Axis: is a line we are rotating around, that is, during the rotation points maintain the same distance from the rotation axis.
• Rotation Plane: During the rotation points in the plain remain in the plane and other points remain the same distance from the plane.

Note: we are talking about rotations about the origin so both the rotation axis and the rotation plane go through the origin.

Imagine a point P1 which is a unit distance from the origin, we will be rotating it through an angle (a) to P3 through midpoint P2.

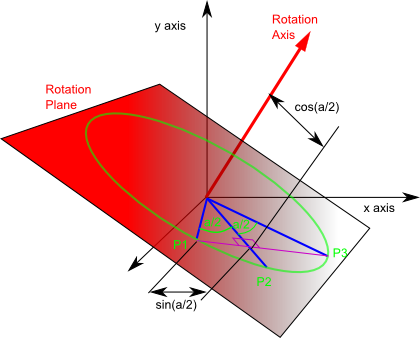
So the point P1 is transformed to P3, if it travels in a straight line it passes through a point cos(a/2) from the rotation axis and sin(a/2) from both P1 and P3.

 

Maths – Transforming Vectors with Quaternions

Camp of the Saints
CampOfTheSaints

Crow-Falls
Crow-Falls

Decent of Sweden
Descent-Of-Sweden

With Open Gates Intro
WithOpenGatesIntro

With Open Gates
WithOpenGates

Winter Chan
Winter-Chan

What it Has to Be Instrumental
What-It-Has-To-Be