Unity Physics 101: Basics of Rigid bodies and Joints from GRID Lab on Vimeo.
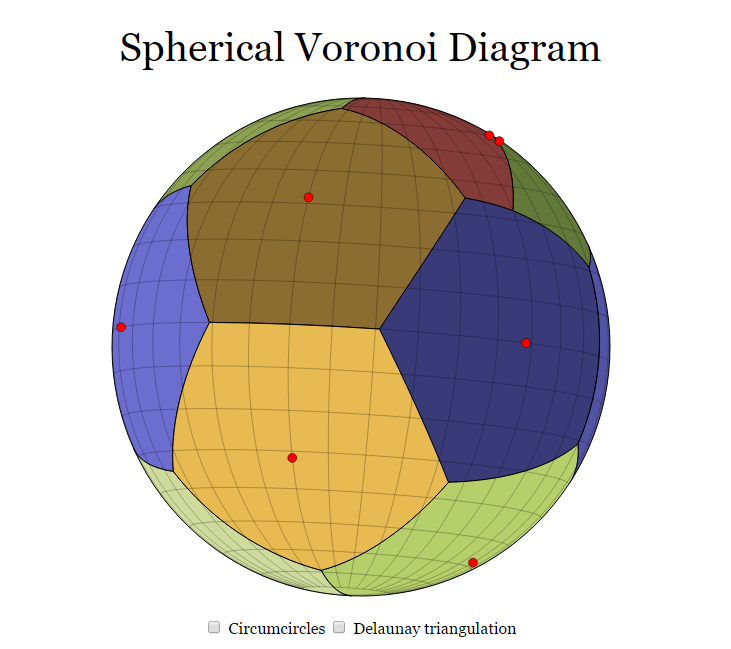
A Plane Sweep Algorithm for the Voronoi Tessellation of the Sphere
STRIPACK
Delaunay Triangulation on a Sphere
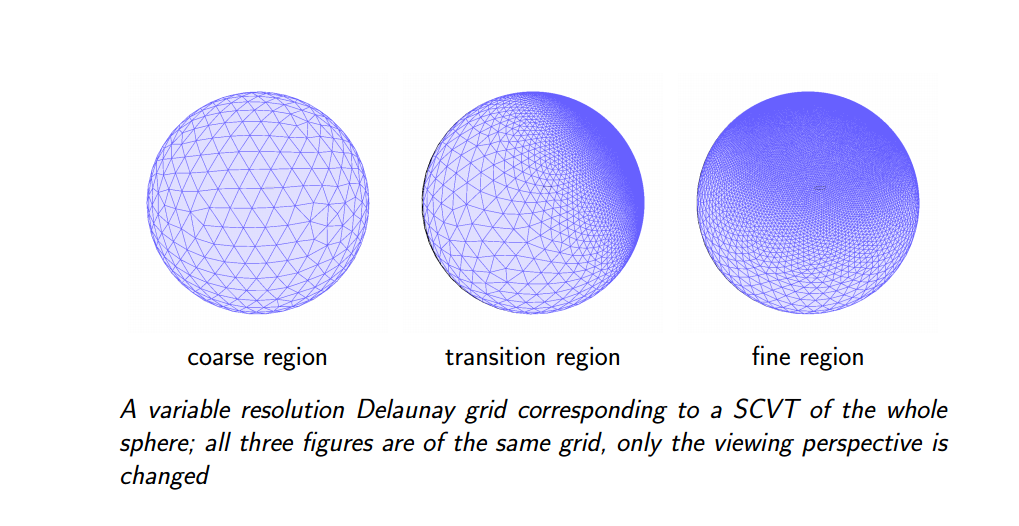
PARALLEL ALGORITHM FOR SPHERICAL DELAUNAY TRIANGULATIONS AND SPHERICAL CENTROIDAL VORONOI TESSELLATIONS
(PDF)
Distribution of Points on a Sphere with Application to Star Catalogs
Covering and packing with spherical caps
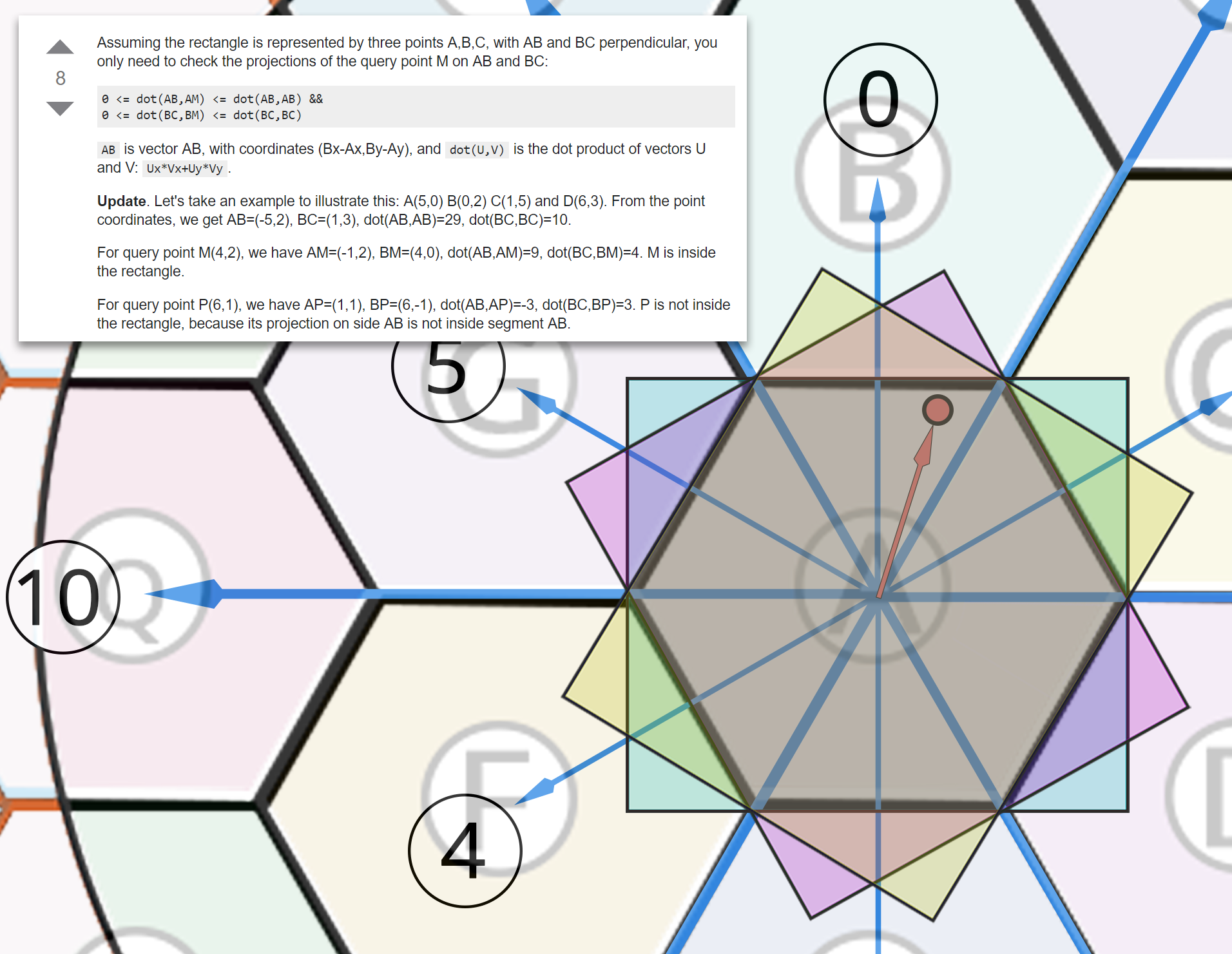
A spherical cap C(x,r)C(x,r) centred at xx with radius rr is the set of all points on the sphere a distance of at most rr from the point xx. For a fixed number of points mm, the packing problem is to find the centres xjxj, j=1,…,mj=1,…,m of mm identical non-overlapping spherical caps so that their common radius is maximized. This packing radius is twice the minimum angle between the points. The set of points is called a spherical code. The problem of finding a point set to maximize the minimum angle between the points is known as Tammes problem after his work on pollen grains in 1930 or the Fejes Toth problem (he proved an upper bound on the minimum distance between points in 1943). A related problem is the Kepler Conjecture (1611) that the densest packing of hard spheres in three dimensional space is hexagonal close packing with a density of around 74.048% (reportedly proved by Hales in 1998 taking some 282 pages).
On the other hand the covering problem is to find the centres xjxj, j=1,…,mj=1,…,m of mm identical spherical caps which completely cover the sphere so that their common radius is minimized. This covering radius is given by the distance of the furthest point on the sphere from the closest point in the set xjxj, j=1,…,mj=1,…,m , which is also known as the mesh norm. The mesh norm can be calculated using the Voronoi cells or Delaunay triangulation. Another measure of the equidistribution of a point set is the ratio (always greater than 1) of the covering radius to the packing radius. The figure of the left gives the spherical packing for this set of points, the middle figure the distance of the point from the closest point in the set (the mesh norm is the global maximum of this function) and the figure on the right gives the spherical covering.
Inheritance – Solved by adding Quad in constructor
[ArgosMeshDraft.cs]
using UnityEngine;
using System;
using System.Collections;
using ProceduralToolkit;
using System.Collections.Generic;
namespace ProceduralToolkit
{
public class ArgosMeshDraft : MeshDraft
{
public List<Vector3> vTriCenter = new List<Vector3>();
public List<int> vQual = new List<int>();
public ArgosMeshDraft()
{
Color col = new Color(1, 1, 1, 1);
Add(Quad(Vector3.zero, Vector3.zero, Vector3.zero, col));
}
}
}
[Cosahedra.cs]
using UnityEngine;
using System.Collections;
using ProceduralToolkit;
using UnityEngine.UI;
using System.Collections.Generic;
public class Cosahedra : MonoBehaviour
{
public Text NumTrisText;
public float radius = 1.5f;
public ArgosMeshDraft aMD = new ArgosMeshDraft();
public ArgosMeshDraft aMD_IcosaSphere = new ArgosMeshDraft();
MeshDraft mD_Tri = new MeshDraft();
int depth = 4;
void Start ()
{
aMD.Clear();
aMD.Add(MeshDraft.Icosahedron(radius));
aMD_IcosaSphere.Clear();
Create_GP(depth);
GetComponent<MeshFilter>().mesh = aMD_IcosaSphere.ToMesh();
}
public void writeMesh()
{
GetComponent<MeshFilter>().mesh = aMD_IcosaSphere.ToMesh();
}
public ArgosMeshDraft getArgosMeshDraft()
{
return aMD_IcosaSphere;
}
void Update ()
{
}
void Create_GP(int depth)
{
for(int i = 0; i<20; i++)
{
Vector3 v0 = aMD.vertices[aMD.triangles[i*3]];
Vector3 v1 = aMD.vertices[aMD.triangles[i*3 +1]];
Vector3 v2 = aMD.vertices[aMD.triangles[i*3 + 2]];
Color col = getWhite();
subdivide(v0, v1, v2, depth, col);
}
}
void addTriangle(Vector3 v0, Vector3 v1, Vector3 v2, Color col)
{
mD_Tri.Clear();
mD_Tri = MeshDraft.Triangle(v0, v1, v2);
mD_Tri.Paint(col);
aMD_IcosaSphere.Add(mD_Tri);
}
void subdivide(Vector3 v1, Vector3 v2, Vector3 v3, int depth, Color col)
{
Vector3 v12, v23, v31;
Vector3 v12_n, v23_n, v31_n;
int i;
if (depth == 0)
{
addTriangle(v1, v2, v3, col);
return;
}
v12 = (v1 + v2) / 2.0f;
v23 = (v2 + v3) / 2.0f;
v31 = (v3 + v1) / 2.0f;
/* extrude midpoints to lie on unit sphere */
v12_n = v12.normalized * radius;
v23_n = v23.normalized * radius;
v31_n = v31.normalized * radius;
/* recursively subdivide new triangles */
subdivide(v1, v12_n, v31_n, depth - 1, col);
subdivide(v2, v23_n, v12_n, depth - 1, col);
subdivide(v3, v31_n, v23_n, depth - 1, col);
subdivide(v12_n, v23_n, v31_n, depth - 1, col);
}
Color getIDXolor(int i)
{
Color col;
col.r = 0.2f + (float)(i) * 0.8f / 20f ;
col.g = 0.5f + (float)(i) * 0.5f / 20f;
col.b = 1f - (float)(i) * 0.8f / 20f;
col.a = 1f;
return col;
}
Color getWhite() // :)
{
Color col;
col.r = 1f;
col.g = 1f;
col.b = 1f;
col.a = 1f;
return col;
}
Color getINColor(int i)
{
Color col;
col.r = (float)(i) / 1024f;
col.g = 1f - (float)(i) / 1024f;
col.b = 0.5f - (float)(i) / 1024f;
if(col.b>0) col.b = 1f- (float)(i) / 1024f;
col.a = 1f;
return col;
}
}

Vector2[] rota = new[] {
new Vector2(-1, 0),
new Vector2(-0.5f, Mathf.Sqrt(3f)/2f),
new Vector2(0.5f, Mathf.Sqrt(3f)/2f),
new Vector2(1, 0),
new Vector2(0.5f, -Mathf.Sqrt(3f)/2f),
new Vector2(-0.5f, -Mathf.Sqrt(3f)/2f),
new Vector2( -Mathf.Sqrt(3f)/2f, 0.5f),
new Vector2(0, 1),
new Vector2( Mathf.Sqrt(3f)/2f,0.5f),
new Vector2( Mathf.Sqrt(3f)/2f,-0.5f),
new Vector2(0, -1),
new Vector2(- Mathf.Sqrt(3f)/2f,-0.5f) };
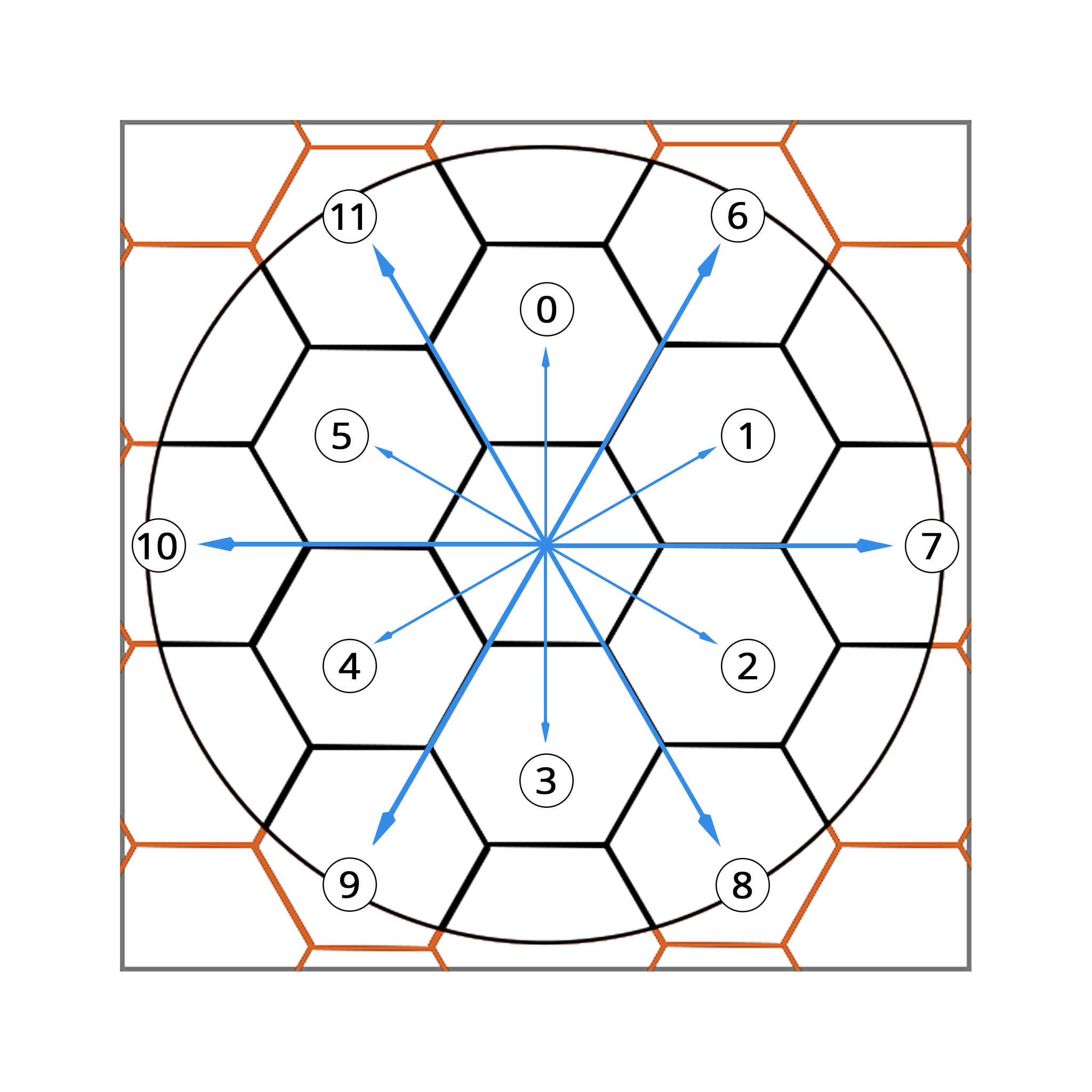
public void onUV_Indexed_Paint(int i)
{
float scaleFactor = 1;
float dir = 1;
Angle_to_Rotate = 360 / (float)NUM_cells_Circ;
if ((i > 5 && i<12) || (i> 17 && i < 24))
{
scaleFactor = Mathf.Sqrt(3);
}
if (i > 11)
{
dir = -1f;
i -= 12;
}
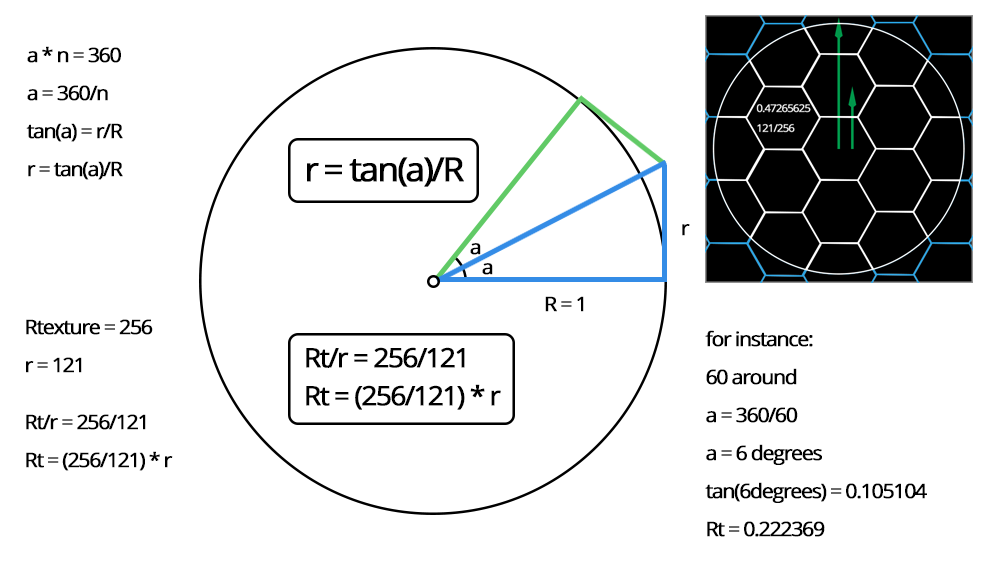
float r = Mathf.Tan(2f * Mathf.PI * Angle_to_Rotate / 360f) / cosaHedra.radius;
fRadius_UV = (256f / 121f) * r;
float angleX = rota[i].x * Angle_to_Rotate * scaleFactor * dir;
float angleY = rota[i].y * Angle_to_Rotate * scaleFactor * dir;
transform.Rotate(angleX, 0, 0);
transform.Rotate(0, angleY, 0);
Paint_UV();
}
public void Paint_UV()
{
Vector3 cPos = transform.forward*cosaHedra.radius;
ICO_MeshDraft = cosaHedra.getMeshDraft();
List<int> tL = ICO_MeshDraft.triangles;
List<Vector3> vL = ICO_MeshDraft.vertices;
List<Vector2> uvL = ICO_MeshDraft.uv;
int numVerts = tL.Count;
Vector3 vToLoc;
Vector2[] uv = new Vector2[3];
bool reject = false;
Vector3 vC;
Vector3 vIn;
Vector3 vUp;
Vector3 vRight;
float x, y;
for (int i = 0; i < numVerts - 2; i += 3)
{
vC = (vL[tL[i]] + vL[tL[i + 1]] + vL[tL[i + 2]]) / 3f;
vToLoc = vC - cPos;
if (vToLoc.magnitude < 1.414 * fRadius_UV)
{
for (int k = i; k < i + 3; k++)
{
vUp = transform.up;
vIn = vL[tL[k]].normalized;
vRight = Vector3.Cross(vUp, vIn);
Vector3.Normalize(vRight);
vUp = Vector3.Cross(vIn, vRight);
vToLoc = vL[tL[k]] - cPos;
vToLoc /= fRadius_UV * 2;
x = 0.5f + Vector3.Dot(vToLoc, vRight);
y = 0.5f + Vector3.Dot(vToLoc, vUp);
if (x >= 0 && x <= 1 && y >= 0 && y <= 1)//Check if each triangle vertex ia within bounds of texture
{
uv[k - i] = new Vector2(x, y);
}
else reject = true;
}
if (!reject)
{
for (int k = i; k < i + 3; k++)
{
uvL[tL[k]] = uv[k - i];
}
}
reject = false;
}
}
cosaHedra.writeMesh();
}