/*
15-462 Computer Graphics I
Lecture 8: Shading in OpenGL
[Angel, Ch. 6.6-6.9]
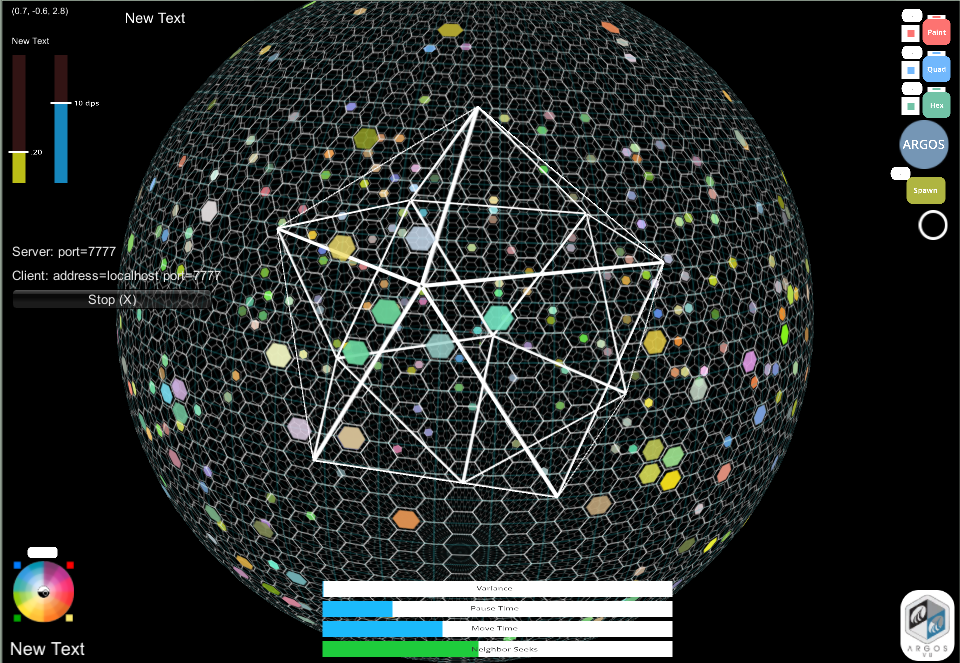
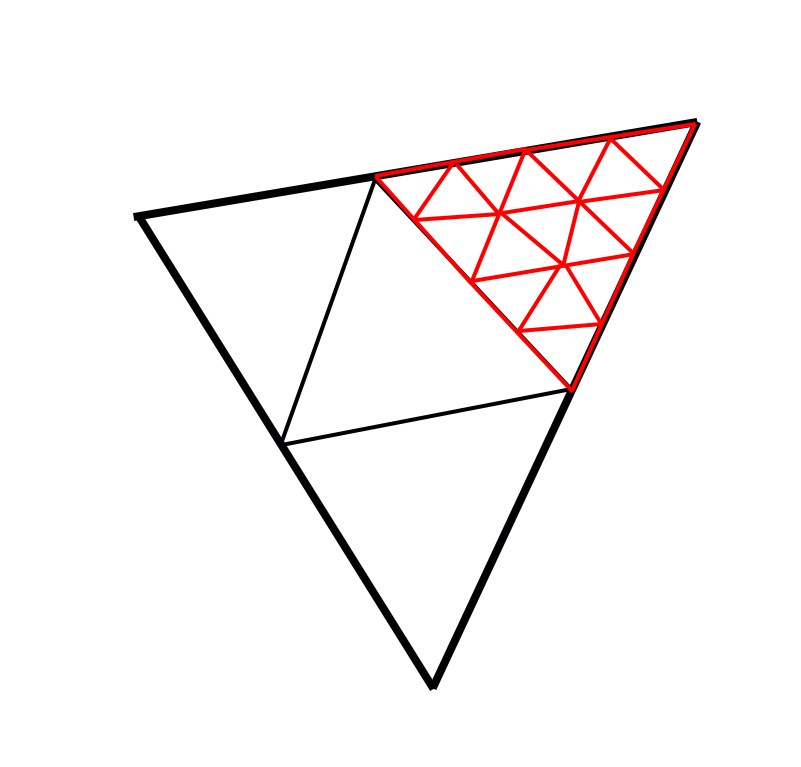
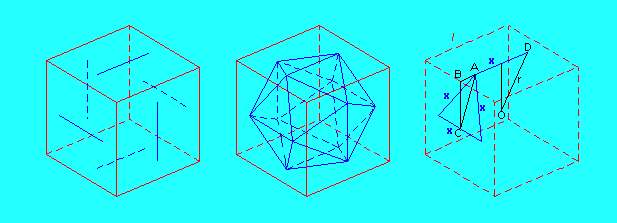
Drawing an icosahedron
Subdividing an icosahedron to approximate a sphere
Based on OpenGL programming guide
Modified: Frank Pfenning
*/
/*
Keyboard inputs:
+ increase subdivision depth
- decrease subdivision depth
f flat shading (regular object)
s smooth shading (approximate sphere)
q quit
*/
#include <stdlib.h>
#include <math.h>
#include <GL/glut.h>
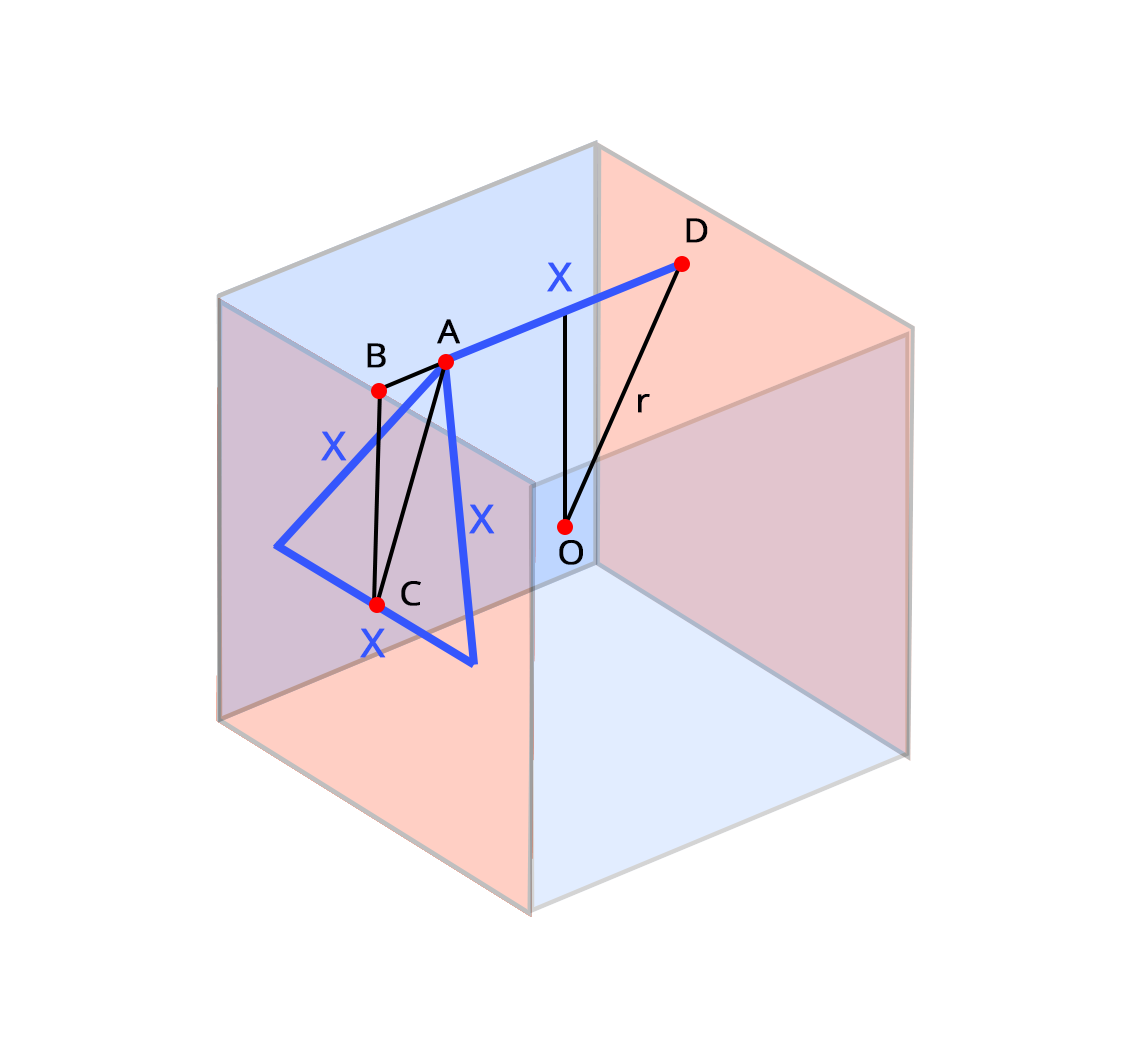
#define X 0.525731112119133696
#define Z 0.850650808352039932
/* vertex data array */
static GLfloat vdata[12][3] = {
{-X, 0.0, Z}, {X, 0.0, Z}, {-X, 0.0, -Z}, {X, 0.0, -Z},
{0.0, Z, X}, {0.0, Z, -X}, {0.0, -Z, X}, {0.0, -Z, -X},
{Z, X, 0.0}, {-Z, X, 0.0}, {Z, -X, 0.0}, {-Z, -X, 0.0}
};
/* triangle indices */
static int tindices[20][3] = {
{1,4,0}, {4,9,0}, {4,5,9}, {8,5,4}, {1,8,4},
{1,10,8}, {10,3,8}, {8,3,5}, {3,2,5}, {3,7,2},
{3,10,7}, {10,6,7}, {6,11,7}, {6,0,11}, {6,1,0},
{10,1,6}, {11,0,9}, {2,11,9}, {5,2,9}, {11,2,7}
};
GLfloat mat_specular[] = {0.0, 0.0, 0.0, 1.0};
GLfloat mat_diffuse[] = {0.8, 0.6, 0.4, 1.0};
GLfloat mat_ambient[] = {0.8, 0.6, 0.4, 1.0};
GLfloat mat_shininess = 100.0; /* unused if specular is 0 */
GLfloat light_ambient[] = {0.2, 0.2, 0.2, 1.0};
GLfloat light_diffuse[] = {1.0, 1.0, 1.0, 1.0};
GLfloat light_specular[] = {0.0, 0.0, 0.0, 1.0};
GLfloat light_position[] = {1.5, 1.0, -2.0, 0.0}; /* directional */
int flat = 1; /* 0 = smooth shading, 1 = flat shading */
int subdiv = 0; /* number of subdivisions */
/* normalize a vector of non-zero length */
void normalize(GLfloat v[3])
{
GLfloat d = sqrt(v[0]*v[0] + v[1]*v[1] + v[2]*v[2]);
/* omit explict check for division by zero */
v[0] /= d; v[1] /= d; v[2] /= d;
}
/* normalized cross product of non-parallel vectors */
void normCrossProd (GLfloat u[3], GLfloat v[3], GLfloat n[3])
{
n[0] = u[1]*v[2] - u[2]*v[1];
n[1] = u[2]*v[0] - u[0]*v[2];
n[2] = u[0]*v[1] - u[1]*v[0];
normalize(n);
}
void normFace(GLfloat v1[3], GLfloat v2[3], GLfloat v3[3])
{
GLfloat d1[3], d2[3], n[3];
int k;
for (k = 0; k < 3; k++) {
d1[k] = v1[k] - v2[k];
d2[k] = v2[k] - v3[k];
}
normCrossProd(d1, d2, n);
glNormal3fv(n);
}
/* draw triangle using face normals */
void drawTriangleFlat(GLfloat v1[3], GLfloat v2[3], GLfloat v3[3])
{
glBegin(GL_TRIANGLES);
normFace(v1, v2, v3);
glVertex3fv(v1);
glVertex3fv(v2);
glVertex3fv(v3);
glEnd();
}
/* draw triangle using sphere normals */
void drawTriangleSmooth(GLfloat v1[3], GLfloat v2[3], GLfloat v3[3])
{
glBegin(GL_TRIANGLES);
glNormal3fv(v1);
glVertex3fv(v1);
glNormal3fv(v2);
glVertex3fv(v2);
glNormal3fv(v3);
glVertex3fv(v3);
glEnd();
}
/* recursively subdivide face `depth' times */
/* and draw the resulting triangles */
void subdivide(GLfloat v1[3], GLfloat v2[3], GLfloat v3[3], int depth)
{
GLfloat v12[3], v23[3], v31[3];
int i;
if (depth == 0) {
if (flat == 1)
drawTriangleFlat(v1, v2, v3);
else
drawTriangleSmooth(v1, v2, v3);
return;
}
/* calculate midpoints of each side */
for (i = 0; i < 3; i++) {
v12[i] = (v1[i]+v2[i])/2.0;
v23[i] = (v2[i]+v3[i])/2.0;
v31[i] = (v3[i]+v1[i])/2.0;
}
/* extrude midpoints to lie on unit sphere */
normalize(v12);
normalize(v23);
normalize(v31);
/* recursively subdivide new triangles */
subdivide(v1, v12, v31, depth-1);
subdivide(v2, v23, v12, depth-1);
subdivide(v3, v31, v23, depth-1);
subdivide(v12, v23, v31, depth-1);
}
void display(void)
{
int i;
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt(0.5, 0.5, -1.5, /* eye */
0.0, 0.0, 0.0, /* at */
0.0, 1.0, 0.0); /* up */
glLightfv(GL_LIGHT0, GL_POSITION, light_position);
/* drawIco(); */
/* drawSphere(); */
for (i = 0; i < 20; i++) {
subdivide(&vdata[tindices[i][0]][0],
&vdata[tindices[i][1]][0],
&vdata[tindices[i][2]][0],
subdiv);
}
glFlush();
}
void reshape(int w, int h)
{
GLfloat aspect = (GLfloat) w / (GLfloat) h;
glViewport(0, 0, w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-1.25, 1.25, -1.25 * aspect, 1.25 * aspect, -2.0, 2.0);
else
glOrtho(-1.25 * aspect, 1.25 * aspect, -1.25, 1.25, -2.0, 2.0);
glMatrixMode(GL_MODELVIEW);
glutPostRedisplay();
}
void init()
{
glClearColor(0.0, 0.0, 0.0, 0.0);
glLightfv(GL_LIGHT0, GL_AMBIENT, light_ambient);
glLightfv(GL_LIGHT0, GL_DIFFUSE, light_diffuse);
glLightfv(GL_LIGHT0, GL_SPECULAR, light_specular);
glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
glMaterialfv(GL_FRONT, GL_AMBIENT, mat_ambient);
glMaterialfv(GL_FRONT, GL_DIFFUSE, mat_diffuse);
glMaterialf(GL_LIGHT0, GL_SHININESS, mat_shininess);
glShadeModel(GL_SMOOTH); /* enable smooth shading */
glEnable(GL_LIGHTING); /* enable lighting */
glEnable(GL_LIGHT0); /* enable light 0 */
glEnable(GL_DEPTH_TEST);
}
void keyboard(unsigned char key, int x, int y)
{
if (key=='q') exit(0);
if (key=='+') subdiv++;
if (key=='-') subdiv--;
if (key=='f') flat = 1;
if (key=='s') flat = 0;
if (subdiv<0) subdiv = 0;
glutPostRedisplay();
}
int main(int argc, char **argv)
{
/* create window */
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_RGB | GLUT_DEPTH); /* single buffering */
glutInitWindowSize(500, 500);
glutCreateWindow("Subdivide");
/* set callbacks */
glutReshapeFunc(reshape);
glutDisplayFunc(display);
glutKeyboardFunc(keyboard);
/* initialize GL */
init();
glutMainLoop();
return(0);
}


Handle Argos_Sphere Rotation r(t) for tweened quaternions